Overview
Our device is a JJ electrostatically defined in MATBG, with a twist angle of 1.06∘ ± 0.04∘, also studied in reference18 (Fig. 1a). The global carrier density n, tuned by the back gate, is set to…
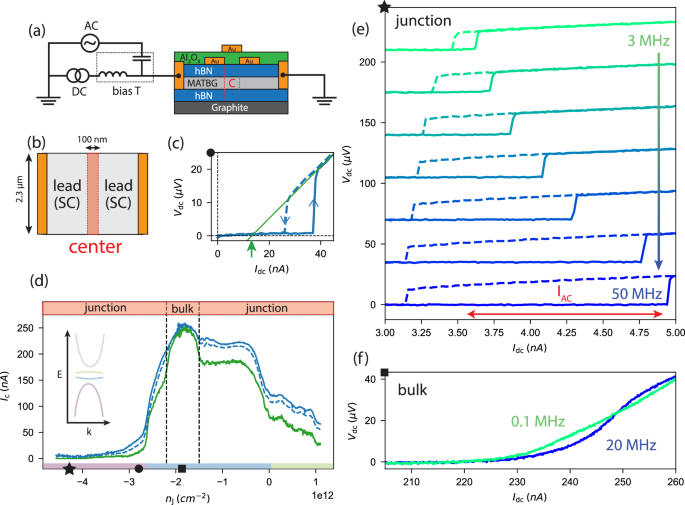
Our device is a JJ electrostatically defined in MATBG, with a twist angle of 1.06∘ ± 0.04∘, also studied in reference18 (Fig. 1a). The global carrier density n, tuned by the back gate, is set to…
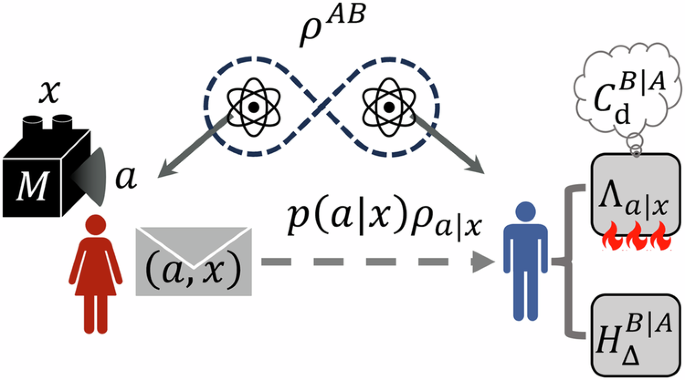
For convenience, we define the optimal conditional distillable coherence and the conditional Shannon entropy as
$${C}_{{\rm{d}}}^{\star }({\mathcal{A}}):=\mathop{\max }\limits_{x}{C}_{{\rm{d}}}^{B|…
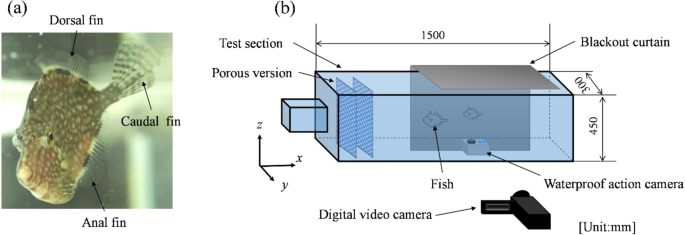
Experiments were conducted at the Yatsukaho Research Campus of Kanazawa Institute of Technology, in compliance with the Animal Welfare Law and related regulations, and after verifying Kanazawa Institute of…
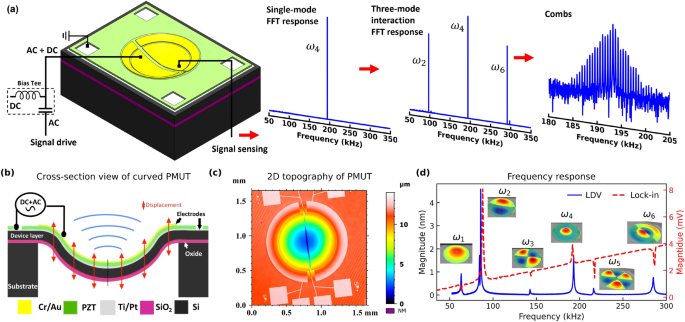
In this work, a curved PMUT is used as a MEMS resonator to demonstrate phononic frequency combs. Figure 1a shows a 3D schematic of the curved PMUT with a four top electrodes configuration and a generalized…
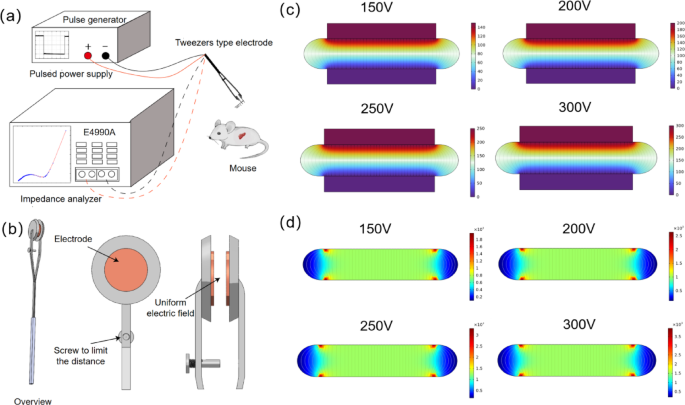
The experimental system setup used is shown in Fig. 1a, and consists of a biomedical pulse generator (BPG300, 3CTEST, Jiangsu, China), an impedance analyzer (E4990A, KEYSIGHT, Penang, Malaysia), and an…
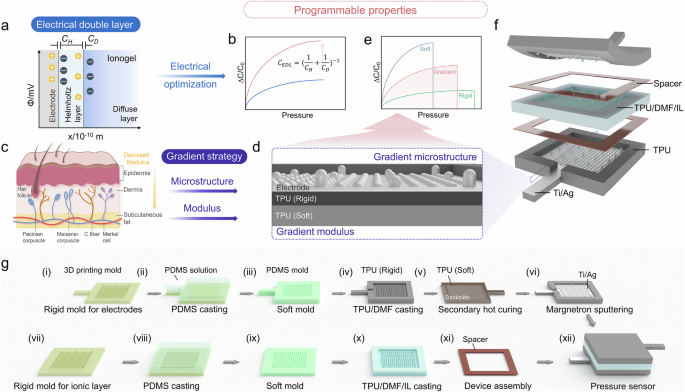
Figure 1a illustrates the working mechanism of EDL based on Gouy–Chapman–Stern model35,36, which are based on the electrostatic interaction and thermal motion of charge carriers37. The EDL…
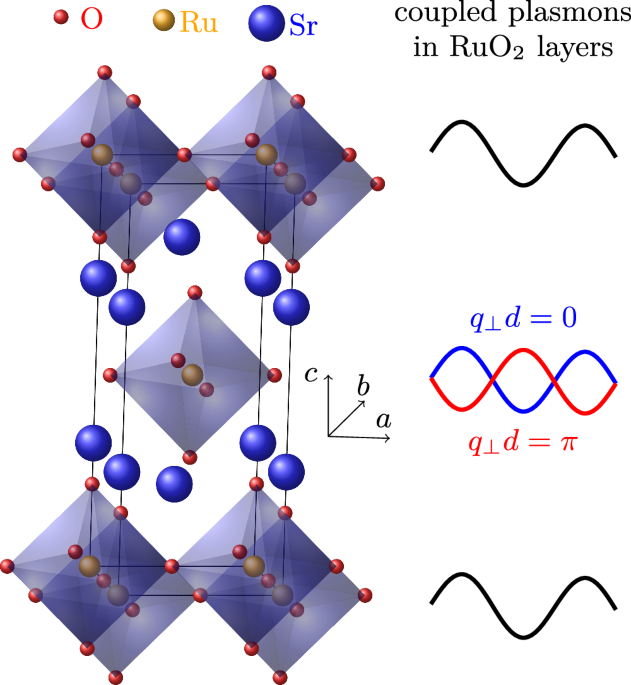
“Strange” metals are at present one of the most interesting research fields in solid state physics1. Due to the strong on-site interaction between their charge carriers, they show a deviation from a Fermi-liquid behavior, e.g., they do not…

Camelliti, P., Borg, T. K. & Kohl, P. Structural and functional characterisation of cardiac fibroblasts. Cardiovasc. Res. 65, 40–51 (2005).
Google Scholar
Kohl, P. &…
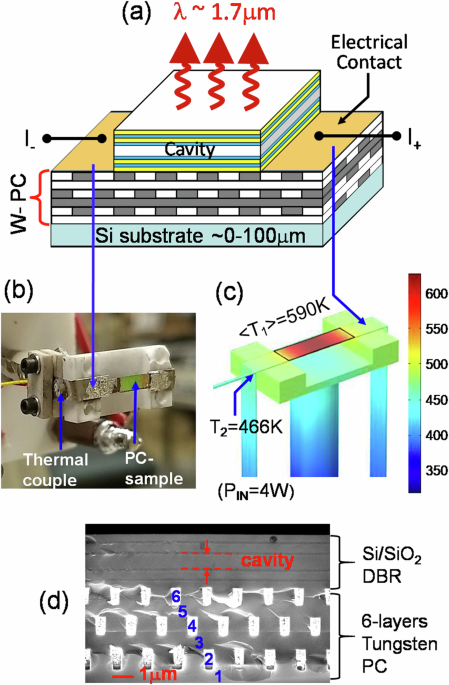
The sample structure used in this experiment has been reported earlier11,24. Briefly, it consists of a micro-cavity fabricated on top of a 3D tungsten-PC (W-PC) on a four-inch silicon wafer. The PC-cavity structure…
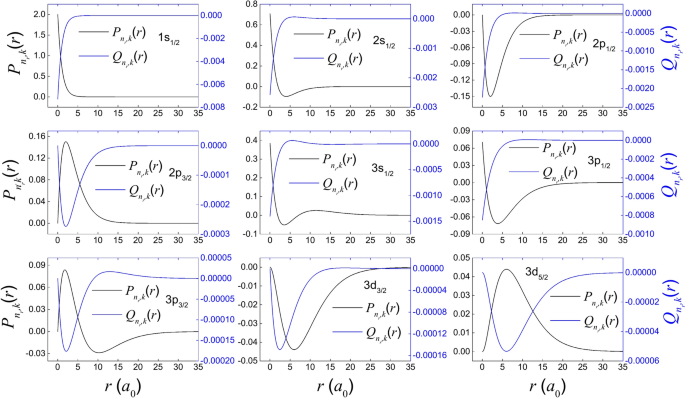
The Dirac Hamiltonian \(H\) for 3D hydrogen atom reads33.
$$H = c\vec{\alpha } \cdot \vec{p} + (\beta – 1)c^{2} + V(r)$$
(1)
where \(\vec{p} = – i\nabla\) is the momentum operator, \(\vec{\alpha }\) and